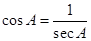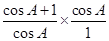NCERT Solutions for Class 10 Maths Ex 8.3

In this post, you will find the NCERT solutions for class 10 maths ex 8.3. These solutions are based on the latest syllabus of NCERT Maths class 10.

NCERT Solutions for Class 10 Maths Ex 8.3

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

 

Solution:  For sin A,

Let us use the identity, cosec² A – cot² A = 1

⇒ cosec² A = 1 + cot² A

⇒ 

⇒ 

⇒ 

For sec A,

Let us use the identity, sec² A – tan² A = 1

⇒ sec² A = 1 + tan² A

⇒  

⇒  

⇒  

For tan A,

2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Solution: For sin A,

Let us use the identity, sin² A + cos² A = 1

⇒ sin² A = 1 – cos² A

⇒ 

⇒ 

For cos A,

For tan A,

Let us use the identity, sec² A – tan² A = 1                 

⇒ tan² A = sec² A – 1

⇒ 

For cot A,

⇒ 

For cosec A,

⇒ 

3. Choose the correct option. Justify your choice.

 (i) 9 sec² A – 9 tan² A =

(A) 1                         (B) 9                         (C) 8                       (D) 0

 

(ii) (1 + tan θ + sec θ) (1 + cot θ  – cosec θ) =

(A) 0                         (B) 1                         (C) 2                        (D) –1

 

(iii) (sec A + tan A) (1 – sin A) =

(A) sec A                  (B) sin A                   (C) cosec A            (D) cos A

(iv) =

(A)  sec² A                   (B)  –1                      (C) cot² A                  (D) tan² A

 

Solution: (i) (B) 9 sec² A  – 9 tan² A

                                                       = 9(sec² A  – tan² A)

                                                       = 9 × 1 = 9

(ii) (C) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

                            = 

                            = 

                            = 

                            = 

                            =           [Since, sin²θ +cos²θ =1]

                            = 

                            = 2

(iii) (D) (sec A + tan A) (1 – sin A)

                               = 

                               = 

                               =     [Since, 1 – sin² A = cos² A]

(iv) (D) 

                                = 

                                = tan² A

4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) 

(ii) 

(iii) 

(iv)

(v) , using the identity cosec²A = 1 + cot²A.

(vi) 

(vii) 

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A

(ix) (cosec A – sin A) (sec A – cos A)

(x) 

Solution: (i) L.H.S. = (cosec θ – cot θ)²

                                 = cosec² θ + cot² θ – 2 cosec θ cot θ

                                 = 

                                 = 

                                 = 

  =           [Since, a² + b² – 2ab = (a – b)²]

                                 = 

                                 = 

                                  = 

                                  = R.H.S.

(ii) L.H.S. = 

                  = 

                  = 

                  =                        [Since, sin² θ + cos² θ = 1]

                  = 

                  = 2/cos A = 2 sec A = R.H.S.

(iii) L.H.S. =

                  =

                  =

                  =

                  =

                  =

                  =

                                  [Since, a³ – b³ = (a –b) (a² + b² + ab)]

                  =     [Since, sin² θ + cos² θ = 1]

                  =

                = 1 + sec θ cosec θ

(iv) L.H.S. =

 

=  

= 1 + cos A

= 

= 

=  

= R.H.S.

(v) L.H.S. = 

Dividing all the terms by sin A, we get

= 

= 

= 

= 

= cot A + cosec A 

= R.H.S.

(vi) L.H.S. = 

=

=              [Since, (a + b)(a – b) = a² – b²]

=               [Since, 1 – sin² θ = cos² θ]

= 

= sec A + tan A 

= R.H.S.

(vii) L.H.S. = 

= 

=    [Since, 1 – sin² θ = cos² θ]

= 

= 

= tan θ 

= R.H.S.

(viii) L.H.S. = (sin A + cosec A)² + (cos A + sec A)²

= 

= 

= 

= 

= 5 + cosec² A + sec² A

= 5 + 1 + cot² A + 1 + tan² A

[Since, cosec² θ = 1 + cot² θ and sec² θ = 1 + tan² θ]

= 7 + tan² A + cot² A

= R.H.S.

(ix) L.H.S. = (cosec A – sin A) (sec A – cos A)

= 

= 

= 

= sin A cos A

=                      [Since, sin² θ + cos² θ = 1]

Dividing the numerator and the denominator by sin A cos A, we get

= 

= 

=  

= R.H.S.

(x) L.H.S. = 

[Since, 1 + tan² θ = sec² θ and 1 + cot² θ = cosec² θ]

=  

= tan² A = R.H.S.

Now, the middle term = 

=  

= (– tan A)²

= tan² A 

= R.H.S.