Polyhedrons
A polyhedron is a 3-dimensional shape that is formed by polygons. Every
polygon in a polyhedron is called a face.
The faces meet in a line segment that is called an edge.
The point of intersection of three or more edges is called a vertex.
There are two
important members of the polyhedron family: prisms and
pyramids.
Prisms and pyramids are polyhedrons but
sphere, cone and cylinder are not polyhedrons because their faces are not
polygons.
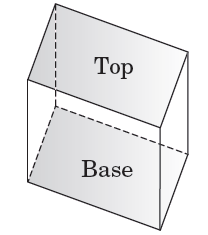
Prism
A solid shape having
its base and top as identical polygons and side faces as rectangles is called a
prism. For example, a cube, a cuboid, etc.
Pyramid
A solid shape having its base as any polygon
and side faces as triangles with a common vertex is called a pyramid.
For example, a triangular pyramid
(tetrahedron), a square pyramid, etc.
Types of Prisms
Triangular Prism
A prism having
its base and top as identical triangles and side faces as rectangles is called
a triangular prism. A triangular
prism has 5 faces, 6 vertices and 9 edges.
Square Prism
If the base and top of a prism are identical
squares, then it is called a square
prism.
A square prism has 6 faces, 8 vertices and
12 edges.
Cube
If a square prism has all of its faces as identical
squares, then it is called a cube.
A cubic prism or a cube has 6 faces, 8
vertices and 12 edges.
Rectangular Prism (Cuboid)
If the base and
top of a prism are identical rectangles, then it is called a rectangular prism or a cuboid. A cuboid
has 6 faces, 8 vertices and 12 edges.
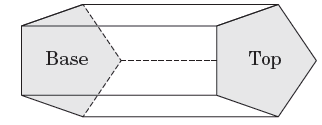
Pentagonal Prism
If the base and top of a prism are identical
pentagons, then it is called a pentagonal
prism. A pentagonal prism has 7 faces, 10 vertices and 15 edges.
Types of Pyramids
All lateral
faces of a pyramid are triangles and it is named according to the number of
sides of its base.
Triangular Pyramid (Tetrahedron)
If
the base of a pyramid is a triangle, then it is called a triangular pyramid. A triangular pyramid is also called a tetrahedron.
A
triangular pyramid has 4 faces, 4 vertices and 6 edges.
Square Pyramid
A pyramid with a square base is called a square pyramid. A square pyramid has 5
faces, 5 vertices and 8 edges.
Rectangular Pyramid
If the base of a pyramid is a rectangle,
then it is called a rectangular pyramid.
It has 5 faces, 5 vertices and 8 edges.
Pentagonal Pyramid
If the base of a pyramid is a pentagon, then
it is called a pentagonal pyramid.
It has 6 faces, 6 vertices and 10 edges.
Naming a Polyhedron
The
following table shows the name given to a polyhedron according to the number of
its faces.
|
Number of faces of the polyhedron
|
Name of the polyhedron
|
|
4
|
Tetrahedron
|
|
5
|
Pentahedron
|
|
6
|
Hexahedron
|
|
7
|
Heptahedron
|
|
8
|
Octahedron
|
|
9
|
Nonahedron
|
|
10
|
Decahedron
|
Regular Polyhedron or Platonic Solid
If all the faces of a
polyhedron are regular polygons, then it is called a regular
polyhedron.
There are 5 regular polyhedrons, called as platonic solids.
It is important to note that the platonic solids have a name based on the
number of sides except a cube.
These are:
Tetrahedron: It is a 4-faced
polyhedron such that all the faces are equilateral triangles.
Cube:
It
is a 6-faced polyhedron whose all the faces are squares.
Octahedron:
It
is an 8-faced polyhedron whose all the faces are equilateral triangles.
Dodecahedron:
It
is a 12-faced polyhedron whose all the faces are regular pentagons.
Icosahedron: It
is a 20-faced polyhedron whose all the faces are equilateral triangles.
Non-polyhedron Prism
A cylinder is a
prism because it has identical circular base and top. But it is not a
polyhedron, because its base is not a polygon. It has 3 faces (2 flat and 1
curved) and 2 edges. It has no corner.
Non-polyhedron Pyramid
The base of a cone is not a polygon,
therefore, it is a pyramid but not a polyhedron. It has 2 faces (1 flat and 1
curved), 1 edge and 1 vertex.
Euler’s
Formula
We can easily count the number of faces, vertices and edges of a
polyhedron, if the number of sides of base is less than 10. But if the number
of sides of base is greater, then counting faces, vertices and edges becomes
difficult. To overcome this difficulty, the great Swiss mathematician Leonard Euler discovered a very
important relationship among the number of faces (F), vertices (V) and edges
(E) of a polyhedron, called Euler’s formula.
According
to Euler’s formula, F + V – E = 2
Example 1: An octahedron has 8 faces and 12 edges. How many vertices
does it have?
Solution:
In the given octahedron, number of faces (F)
= 8 and number of edges (E) = 12.
Let the number of vertices in the given octahedron
be V.
Using Euler’s formula, we have F + V – E = 2
8 + V – 12 = 2
V = 2 – 8 + 12
V
= 6
Thus, the
required number of vertices is 6.
Example 2:
An icosahedron has
30 edges and 12 vertices. How many faces does it have?
Solution:
In the given icosahedron,
number of vertices
(V) = 12 and number of edges (E) = 30.
Let the number of faces in
the given icosahedron
be F.
Using Euler’s formula, we have F + V – E = 2
F + 12 – 30 = 2
F = 2 + 30 – 12
F = 20
Thus, the
required number of faces is 20.